Storing graphs in the database: SQL meets social network

7 September 2009 Technology engineering

Graphs are ubiquitous. Social or P2P networks, thesauri, route planning systems, recommendation systems, collaborative filtering, even the World Wide Web itself is ultimately a graph!

Given their importance, it's surely worth spending some time in studying some algorithms and models to represent and work with them effectively. In this short article, we're going to see how we can store a graph in a DBMS. Given how much attention my talk about storing a tree data structure in the db received, it's probably going to be interesting to many. Unfortunately, the Tree models/techniques do not apply to generic graphs, so let's discover how we can deal with them.

What's a graph

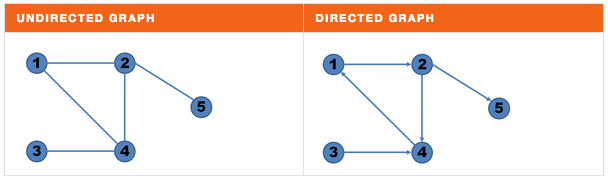
A graph is a set of nodes (vertices) interconnected by links (edges). When the edges have no orientation, the graph is called an undirected graph. In contrast, a graph where the edges have a specific orientation from a node to another is called directed:

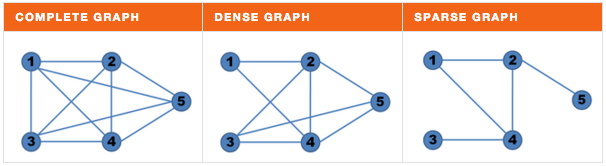
A graph is called complete when there's an edge between any two nodes, dense when the number of edges is close to the maximal number of edges, and sparse when it has only a few edges:

Representing a graph

Two main data structures for the representation of graphs are used in practice. The first is called an adjacency list, and is implemented as an array with one linked list for each source node, containing the destination nodes of the edges that leave each node. The second is a two-dimensional boolean adjacency matrix, in which the rows and columns are the source and destination vertices, and entries in the array indicate whether an edge exists between the vertices. Adjacency lists are preferred for sparse graphs; otherwise, an adjacency matrix is a good choice. [1]

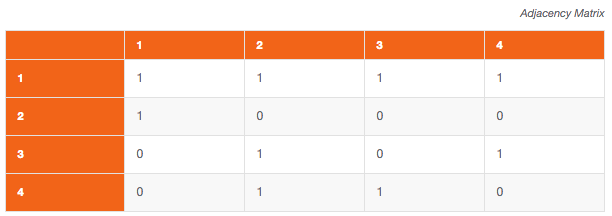
When dealing with databases, most of the times the adjacency matrix is not a viable option, for two reasons: there is a hard limit in the number of columns that a table can have, and adding or removing a node requires a DDL statement.

Joe Celko dedicates a short chapter to graphs in his 'SQL for Smarties' book, but the topic is treated in a quite hasty way, which is surprising given his usual high standards.

One of the basic rules of a successful representation is to separate the nodes and the edges, to avoid DKNF problems. Thus, we create two tables:

CREATE TABLE nodes (
 id INTEGER PRIMARY KEY,
 name VARCHAR(10) NOT NULL,
 feat1 CHAR(1), -- e.g., age
 feat2 CHAR(1)  -- e.g., school attended or company
);
 
CREATE TABLE edges (
 a INTEGER NOT NULL REFERENCES nodes(id) ON UPDATE CASCADE ON DELETE CASCADE,
 b INTEGER NOT NULL REFERENCES nodes(id) ON UPDATE CASCADE ON DELETE CASCADE,
 PRIMARY KEY (a, b)
);
 
CREATE INDEX a_idx ON edges (a);
CREATE INDEX b_idx ON edges (b);

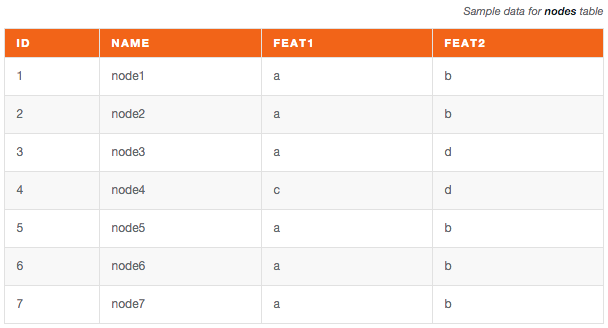
The first table (nodes) contains the actual node payload, with all the interesting information we need to store about a node (in the example, feat1 and feat2 represent two node features, like the age of the person, or the location, etc.).

If we want to represent an undirected graph, we need to add a CHECK constraint on the uniqueness of the pair.

Since the SQL standard does not allow a subquery in the CHECK constraint, we first create a function and then we use it in the CHECK constraint (this example is for PostgreSQL, but can be easily ported to other DBMS):

CREATE FUNCTION check_unique_pair(IN id1 INTEGER, IN id2 INTEGER) RETURNS INTEGER AS $body$
DECLARE retval INTEGER DEFAULT 0;
BEGIN
SELECT COUNT(*) INTO retval FROM (
  SELECT * FROM edges WHERE a = id1 AND b = id2
  UNION ALL
  SELECT * FROM edges WHERE a = id2 AND b = id1
) AS pairs;
RETURN retval;
END
$body$
LANGUAGE 'plpgsql';
 
ALTER TABLE edges ADD CONSTRAINT unique_pair CHECK (check_unique_pair(a, b) < 1);

NB: a UDF in a CHECK constraint might be a bit slow [4]. An alternative is to have a materialized view [5] or force an order in the node pair (i.e. "CHECK (a < b)", and then using a stored procedure to insert the nodes in the correct order).

If we also want to prevent self-loops (i.e. a node linking to itself), we can add another CHECK constraint:

ALTER TABLE edges ADD CONSTRAINT no_self_loop CHECK (a <> b)

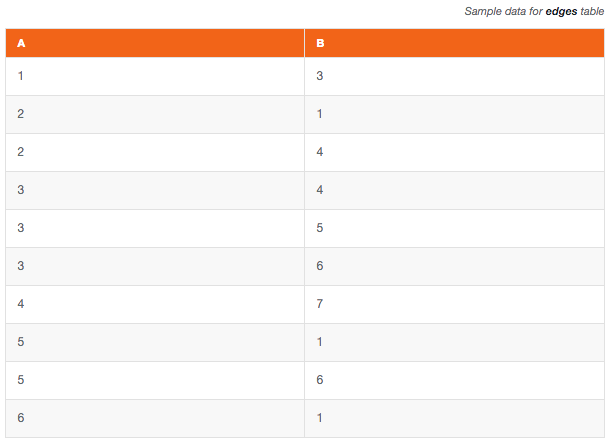
Traversing the graph

Now that we know how to store the graph, we might want to know which nodes are connected. Listing the directly connected nodes is very simple:

SELECT *
  FROM nodes n
  LEFT JOIN edges e ON n.id = e.b
 WHERE e.a = 1;  -- retrieve nodes connected to node 1

or, in the case of undirected edges:

SELECT * FROM nodes WHERE id IN (
  SELECT a FROM edges WHERE b = 1
  UNION
  SELECT b FROM edges WHERE a = 1
);
 
-- or alternatively:
 
SELECT * FROM nodes where id IN (
    SELECT CASE WHEN a = 1 THEN b ELSE a END
      FROM edges
     WHERE 1 IN (a, b)
);

Traversing the full graph usually requires more than a query: we can either loop through the connected nodes, one level a time, or we can create a temporary table holding all the possible paths between two nodes.

We could use Oracle’s CONNECT BY syntax or SQL standard’s Common Table Expressions (CTEs) to recurse through the nodes, but since the graph can contain loops, we’d get errors (unless we’re very careful, as we’ll see in a moment).

Kendall Willets [2] proposes a way of traversing (BFS) the graph using a temporary table. It is quite robust, since it doesn’t fail on graphs with cycles (and when dealing with trees, he shows there are better algorithms available). His solution is just one of the many available, but quite good.

The problem with temporary tables holding all the possible paths is it has to be maintained. Depending on how frequently the data is accessed and updated it might still be worth it, but it’s quite expensive. If you do resort to such a solution, these references may be of use [13] [14].

Before going further in our analysis, we need to introduce a new concept: the transitive closure of a graph.

Transitive closure

The transitive closure of a graph G = (V,E) is a graph G* = (V,E*) such that E* contains an edge (u,v) if and only if G contains a path from u to v.

In other words, the transitive closure of a graph is a graph which contains an edge (u,v) whenever there is a directed path from u to v.

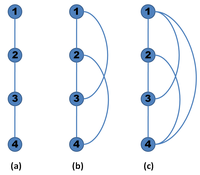
Graph: transitive closure

As already mentioned, SQL has historically been unable [3] to express recursive functions needed to maintain the transitive closure of a graph without an auxiliary table. There are many solutions to solve this problem with a temporary table (some even elegant [2]), but I still haven't found one to do it dynamically.

Here's my clumsy attempt at a possible solution using CTEs

First, this is how we can write the WITH RECURSIVE statement for a Directed (Cyclic) Graph:

WITH RECURSIVE transitive_closure(a, b, distance, path_string) AS
( SELECT a, b, 1 AS distance,
    a || '.' || b || '.' AS path_string
  FROM edges
 
  UNION ALL
 
  SELECT tc.a, e.b, tc.distance + 1,
  tc.path_string || e.b || '.' AS path_string
  FROM edges AS e
    JOIN transitive_closure AS tc
      ON e.a = tc.b
  WHERE tc.path_string NOT LIKE '%' || e.b || '.%'
)
SELECT * FROM transitive_closure
ORDER BY a, b, distance;

Notice the WHERE condition, which stops the recursion in the presence of loops. This is very important to avoid errors.

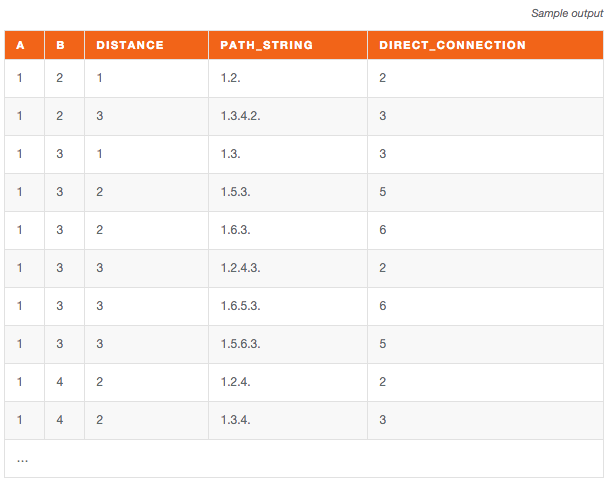
Sample output:

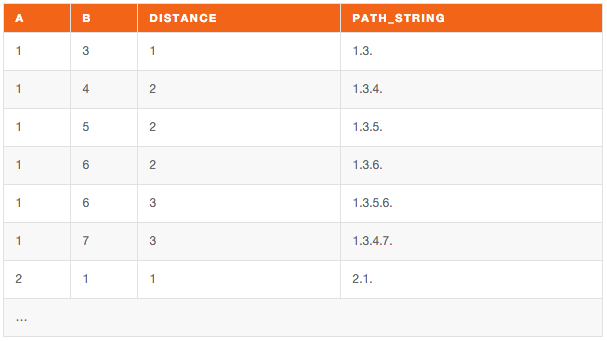
This is a slightly modified version of the same query to deal with Undirected graphs (NB: this is probably going to be rather slow if done in real time):

-- DROP VIEW edges2;
CREATE VIEW edges2 (a, b) AS (
  SELECT a, b FROM edges
  UNION ALL
  SELECT b, a FROM edges
);
 
WITH RECURSIVE transitive_closure(a, b, distance, path_string) AS
( SELECT  a, b, 1 AS distance,
          a || '.' || b || '.' AS path_string
  FROM edges2
 
  UNION ALL
 
  SELECT tc.a, e.b, tc.distance + 1,
  tc.path_string || e.b || '.' AS path_string
  FROM edges2 AS e
    JOIN transitive_closure AS tc ON e.a = tc.b
  WHERE tc.path_string NOT LIKE '%' || e.b || '.%'
)
SELECT * FROM transitive_closure
ORDER BY a, b, distance;

Linkedin: Degrees of separation

One of the fundamental characteristics of networks (or graphs in general) is connectivity. We might want to know how to go from A to B, or how two people are connected, and we also want to know how many "hops" separate two nodes, to have an idea about the distance.

For instance, social networks like LinkedIN show our connections or search results sorted by degree of separation, and trip planning sites show how many flights you have to take to reach your destination, usually listing direct connections first.

There are some database extensions or hybrid solutions like SPARQL on Virtuoso [11] that add a TRANSITIVE clause [12] to make this kind of queries both easy and efficient, but we want to see how to reach the same goal with standard SQL.

As you might guess, this becomes really easy once you have the transitive closure of the graph, we only have to add a WHERE clause specifying what our source and destination nodes are:

WITH RECURSIVE transitive_closure(a, b, distance, path_string) AS
( SELECT a, b, 1 AS distance,
         a || '.' || b || '.' AS path_string
  FROM edges
 WHERE a = 1 -- source
 
  UNION ALL
 
  SELECT tc.a, e.b, tc.distance + 1,
         tc.path_string || e.b || '.' AS path_string
  FROM edges AS e
  JOIN transitive_closure AS tc ON e.a = tc.b
 WHERE tc.path_string NOT LIKE '%' || e.b || '.%'
)
  SELECT * FROM transitive_closure
   WHERE b=6 -- destination
ORDER BY a, b, distance;

If we're showing the trip planning results, then we have a list of all possible travel solutions; instead of sorting by distance, we might sort by price or other parameters with little changes.

If we're showing how two people are connected (LinkedIN), then we can limit the result set to the first row, since we're probably interested in showing the shortest distance only and not all the other alternatives.

Instead of adding a LIMIT clause, it's probably more efficient to add "AND tc.distance = 0" to the WHERE clause of the recursive part of the CTE, or a GROUP BY clause as follows:

WITH RECURSIVE transitive_closure(a, b, distance, path_string)
AS
( SELECT a, b, 1 AS distance,
         a || '.' || b || '.' AS path_string
  FROM edges2
 
  UNION ALL
 
  SELECT tc.a, e.b, tc.distance + 1,
         tc.path_string || e.b || '.' AS path_string
  FROM edges2 AS e
  JOIN transitive_closure AS tc ON e.a = tc.b
 WHERE tc.path_string NOT LIKE '%' || e.b || '.%'
)
SELECT a, b, min(distance) AS dist FROM transitive_closure
--WHERE a = 1 AND b=6
GROUP BY a, b
ORDER BY a, dist, b;

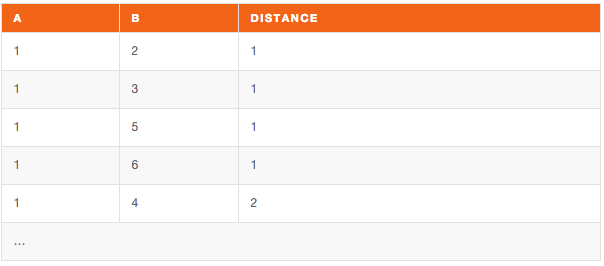
If you are interested in the immediate connections of a certain node, then specify the starting node and a distance equals to one (by limiting the recursion at the first level)

WITH RECURSIVE transitive_closure(a, b, distance, path_string) AS
( SELECT  a, b, 1 AS distance, a || '.' || b || '.' AS path_string
   FROM edges2
  WHERE a = 1 -- set the starting node
 
  UNION ALL
 
  SELECT tc.a, e.b, tc.distance + 1,
  tc.path_string || e.b || '.' AS path_string
  FROM edges2 AS e
    JOIN transitive_closure AS tc ON e.a = tc.b
  WHERE tc.path_string NOT LIKE '%' || e.b || '.%'
    AND tc.distance = 0  -- limit recursion at the first level
)
SELECT b FROM transitive_closure;

Of course to get the immediate connections there's no need for a recursive query (just use the one presented at the previous paragraph), but I thought I'd show it anyway as a first step towards more complex queries.

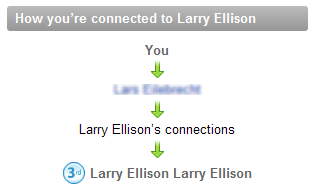
LinkedIN has a nice feature to show "How this user is connected to you" for non directly connected nodes.

If the distance between the two nodes is equal to 2, you can show the shared connections:

SELECT b FROM (
 
WITH RECURSIVE transitive_closure(a, b, distance, path_string) AS
( SELECT  a, b, 1 AS distance, a || '.' || b || '.' AS path_string
   FROM edges2
  WHERE a = 1 -- set the starting node
 
  UNION ALL
 
  SELECT tc.a, e.b, tc.distance + 1,
  tc.path_string || e.b || '.' AS path_string
  FROM edges2 AS e
    JOIN transitive_closure AS tc ON e.a = tc.b
  WHERE tc.path_string NOT LIKE '%' || e.b || '.%'
    AND tc.distance = 0
)
SELECT b FROM transitive_closure
 
UNION ALL
 
(WITH RECURSIVE transitive_closure(a, b, distance, path_string) AS
( SELECT  a, b, 1 AS distance, a || '.' || b || '.' AS path_string
   FROM edges2
  WHERE a = 4 -- set the target node
 
  UNION ALL
 
  SELECT tc.a, e.b, tc.distance + 1,
  tc.path_string || e.b || '.' AS path_string
  FROM edges2 AS e
    JOIN transitive_closure AS tc ON e.a = tc.b
  WHERE tc.path_string NOT LIKE '%' || e.b || '.%'
    AND tc.distance = 0
)
SELECT b FROM transitive_closure
)) AS immediate_connections
GROUP BY b
HAVING COUNT(b) > 1;

In the above query, we select the immediate connections of the two nodes separately, and then select the shared ones.

For nodes having a distance equals to 3, the approach is slightly different.

First, you check that the two nodes are indeed at a minimum distance of 3 nodes (you're probably not interested in showing the relationship between two nodes when the distance is bigger):

WITH RECURSIVE transitive_closure(a, b, distance, path_string) AS
( SELECT a, b, 1 AS distance,
         a || '.' || b || '.' AS path_string
    FROM edges2
   WHERE a = 1 -- set the starting node
 
   UNION ALL
 
  SELECT tc.a, e.b, tc.distance + 1,
         tc.path_string || e.b || '.' AS path_string
    FROM edges2 AS e
    JOIN transitive_closure AS tc ON e.a = tc.b
   WHERE tc.path_string NOT LIKE '%' || e.b || '.%'
     AND tc.distance < 3 -- stop the recursion after 3 levels
)
SELECT a, b, min(distance) FROM transitive_closure
WHERE b=4  -- set the target node
GROUP BY a, b
HAVING min(distance) = 3; --set the minimum distance

Then you select the paths between those nodes.

But there's a different approach which is more generic and efficient, and can be used for all the nodes whose distance is bigger than 2.

The idea is to select the immediate neighbours of the starting node that are also in the path to the other node.

Depending on the distance, you can have either the shared nodes (distance = 2), or the connections that could lead to the other node (distance > 2). In the latter case, you could for instance show how A is connected to B:

WITH RECURSIVE transitive_closure(a, b, distance, path_string) AS
( SELECT a, b, 1 AS distance,
         a || '.' || b || '.' AS path_string,
         b AS direct_connection
    FROM edges2
   WHERE a = 1 -- set the starting node
 
   UNION ALL
 
  SELECT tc.a, e.b, tc.distance + 1,
         tc.path_string || e.b || '.' AS path_string,
         tc.direct_connection
    FROM edges2 AS e
    JOIN transitive_closure AS tc ON e.a = tc.b
   WHERE tc.path_string NOT LIKE '%' || e.b || '.%'
     AND tc.distance < 3
)
SELECT * FROM transitive_closure
--WHERE b=3  -- set the target node
ORDER BY a,b,distance

Facebook: You might also know

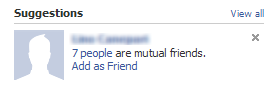
A similar but slightly different requirement is to find those nodes that are most strongly related, but not directly connected yet. In other words, it's interesting to find out which and how many connected nodes are shared between any two nodes, i.e. how many 'friends' are shared between two individuals. Or better yet, to find those nodes sharing a certain (minimum) number of nodes with the current one.

This could be useful to suggest a new possible friend, or in the case of recommendation systems, to suggest a new item/genre that matches the user's interests.

There are many ways of doing this. In theory, this is bordering on the domain of collaborative filtering [6][7][8], so using Pearson's correlation [9] or a similar distance measure with an appropriate algorithm [10] is going to generate the best results. Collaborative filtering is an incredibly interesting topic on its own, but outside the scope of this article.

A rough and inexpensive alternative is to find the nodes having distance equals to 2, and filter those that either have a common characteristic with the source node (went to the same school / worked at the same company, belong to the same interest group / are items of the same genre) or have several mutual 'friends'.

Facebook

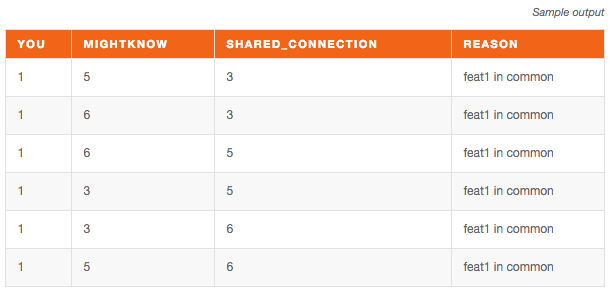
This, again, is easily done once you have the transitive closure of the graph:

SELECT a AS you,
       b AS mightknow,
       shared_connection,
       CASE
         WHEN (n1.feat1 = n2.feat1 AND n1.feat1 = n3.feat1) THEN 'feat1 in common'
         WHEN (n1.feat2 = n2.feat2 AND n1.feat2 = n3.feat2) THEN 'feat2 in common'
         ELSE 'nothing in common'
       END AS reason
  FROM (
WITH RECURSIVE transitive_closure(a, b, distance, path_string) AS
( SELECT a, b, 1 AS distance,
         a || '.' || b || '.' AS path_string,
         b AS direct_connection
    FROM edges2
   WHERE a = 1 -- set the starting node
 
   UNION ALL
 
  SELECT tc.a, e.b, tc.distance + 1,
         tc.path_string || e.b || '.' AS path_string,
         tc.direct_connection
    FROM edges2 AS e
    JOIN transitive_closure AS tc ON e.a = tc.b
   WHERE tc.path_string NOT LIKE '%' || e.b || '.%'
     AND tc.distance < 2
)
SELECT a,
       b,
       direct_connection AS shared_connection
  FROM transitive_closure
 WHERE distance = 2
) AS youmightknow
LEFT JOIN nodes AS n1 ON youmightknow.a = n1.id
LEFT JOIN nodes AS n2 ON youmightknow.b = n2.id
LEFT JOIN nodes AS n3 ON youmightknow.shared_connection = n3.id
WHERE (n1.feat1 = n2.feat1 AND n1.feat1 = n3.feat1)
   OR (n1.feat2 = n2.feat2 AND n1.feat2 = n3.feat2);

Once you have selected these nodes, you can filter those recurring more often, or give more importance to those having a certain feature in common, or pick one randomly (so you don't end up suggesting the same node over and over).

Conclusion

In this article I had some fun with the new and powerful CTEs, and showed some practical examples where they can be useful. I also showed some approaches at solving the challenges faced by any social network or recommendation system.

You are advised that depending on the size of the graph and the performance requirements of your application, the above queries might be too slow to run in realtime. Caching is your friend.

Update: Many of the queries in this article have been revised, so please refer to http://www.slideshare.net/quipo/rdbms-in-the-social-networks-age for changes.